BLS

  • BLS签名算法
    • BLS=Boneh-Lynn-Shacham
    • 概述
      • （常称为）聚合签名算法中的一种
        • 严格的说应该是：pairing-based基于配对的，具备聚合特性的多签名方案
      • 最初是由斯坦福大学教授Dan Boneh等人于2001年提出的一种签名方案，最新是在2018年，Boneh教授与IBM研究机构的Manu Drijvers等人更新了这种签名方案
      • 与以往签名方案不同的是，BLS采用了基于双线性映射的椭圆曲线配对技术，来实现签名验证与聚合
    • BLS签名过程
        1. 准备阶段，秘密选取随机数字作为私钥pk，计算公钥P = pk × G，待签名的消息m。
        1. 签名与验证：将消息哈希H(m)映射到曲线上的点,记为q，将结果点乘以私钥得到签名: S = pk × q
      • 3.验证签名： 按照步骤1同样计算出映射到曲线点q,检验 e(P, q) = e(G, S)
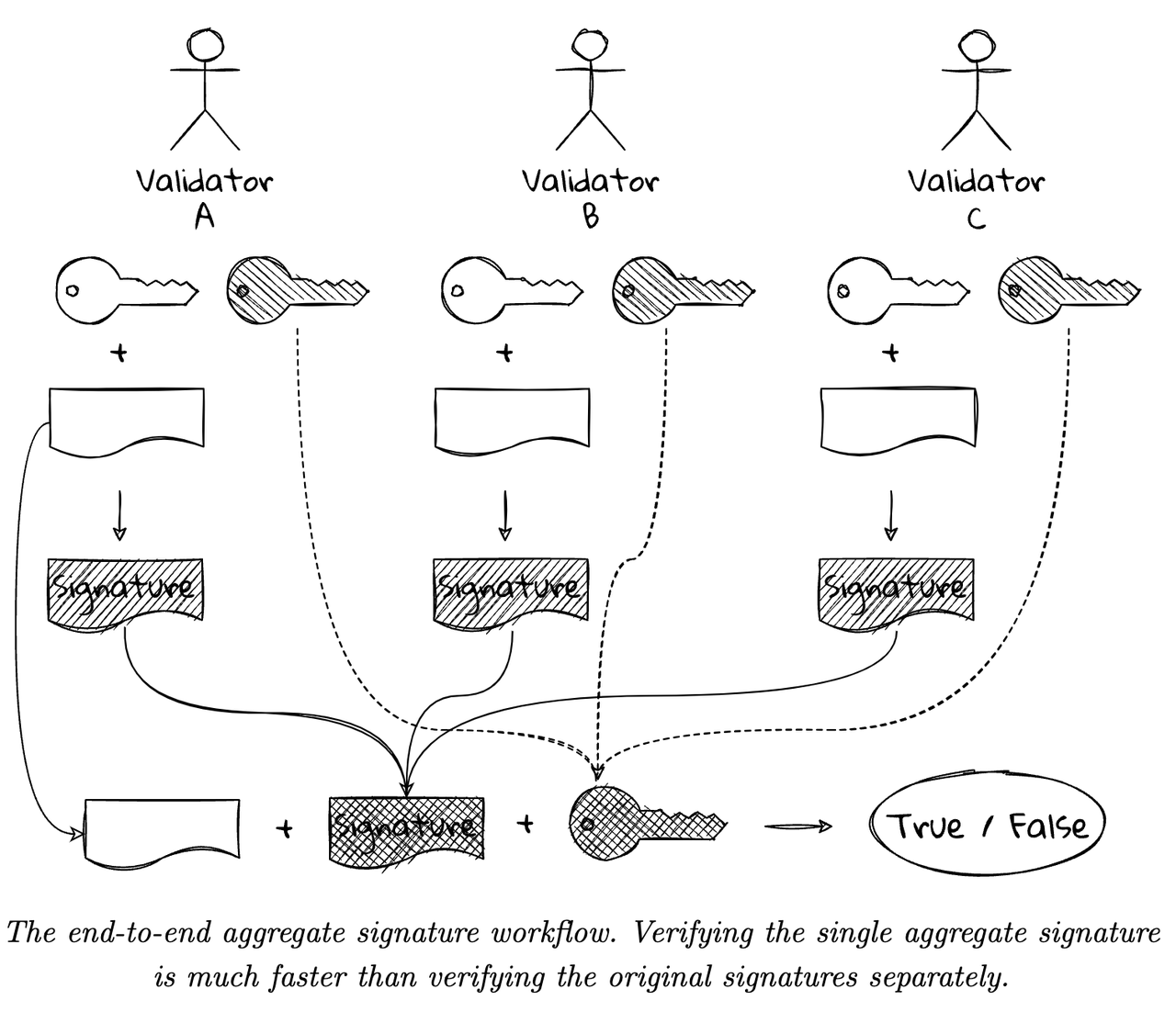
    • 流程图
      • The end-to-end aggregate signature workflow. Verifying the single aggregate signature is much faster than verifying the original signatures separately
        • bls_sig_process
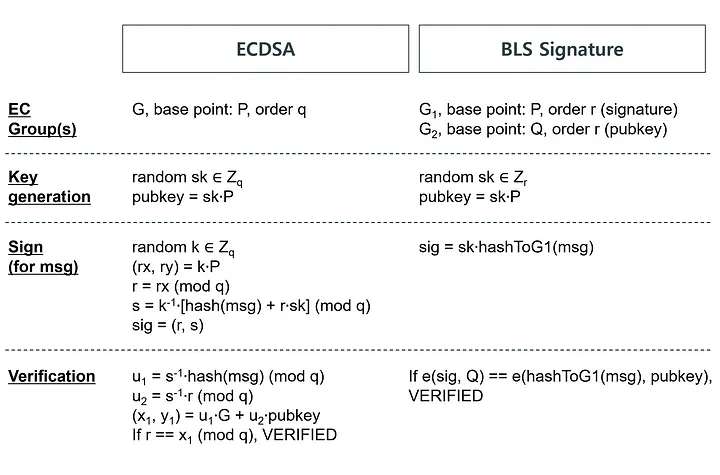
  • 对比
    • ECDSA 和 BLS 签名的算法比较
      • sig_cmp_ecdsa_bls
    • 签名算法
      • ECDSA：对普通数据签名
        • 缺点：无法做签名聚合或者密钥聚合
          • 因此只能挨个对签名进行验证
          • 在验证多重签名的交易时，此举过于繁琐，我们需要逐个验证所有的签名及其对应的公钥，耗费大量的区块空间和交易费
      • Schnorr：可以把一笔交易中的所有签名和公钥合并成单个签名和公钥，且合并过程不可见（无从追溯这个签名或公钥是否通过合并而来）
        • 优点
          • 可以一次性对合并后的签名做验证，加快了区块验证的速度
        • 缺点
          • 多重签名需要多次（签名者之间的）通信，这对冷钱包来说过于麻烦。
          • 聚合签名算法依赖随机数生成器，而不像 ECDSA 那样可以使用指定的随机点（R）
          • m-n 多重签名机制比较取巧，需要构建公钥的默克尔树。当 m 和 n 较大时，树所占空间会相当大。
          • 无法把一个区块中的所有签名聚合成一个签名
      • BLS 签名算法：支持签名聚合或者密钥聚合，且解决了Schnorr签名算法的上述所有问题
        • 优点
          • 不需要随机数生成器
          • 可以将区块中的所有签名聚合成一个，容易实现 m-n 多重签名
          • 避免签名者之间的多余通信
          • （签名的）长度更短（签名为椭圆曲线上的一个点而非两个）
            • 是 Schnorr 或 ECDSA 的 2 分之一

results matching ""

    No results matching ""